Table des matières

I. Dynamique relativiste classique des particules de spin zéro

1. Formalisme Lagrangien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Les équations du mouvement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. La forme non invariante du Lagrangien
    et le temps comme paramètre d'évolution . . . . . . . . . . . . . . . . . . . . . . . .

c. Le Lagrangien invariant et le temps propre comme paramètre d'évolution

2. Formalisme Hamiltonien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. L'Hamiltonien égal à l'énergie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. L'Hamiltonien invariant de valeur numérique nulle . . . . . . . . . . . . . . . . .

3. Les fonctions de Jacobi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Fonction de Jacobi habituelle S₍₁₎ ne contenant pas le temps propre . . . .

b. Premier type de fonction de Jacobi S₍₂₎ contenant le temps propre s . . .

c. Deuxième type de fonction de Jacobi S₍₃₎ contenant le temps propre s

4. Particule libre (absence de champ) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Équation du mouvement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Fonction de Jacobi S₍₁₎ (x_r , x⁽⁰⁾_r) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Fonction de Jacobi S₍₂₎ (x_r , s ; x⁽⁰⁾_r , m) . . . . . . . . . . . . . . . . . . . . . . . .

d. Fonction de Jacobi S₍₃₎ (x_r , s ; x⁽⁰⁾_r , s0) . . . . . . . . . . . . . . . . . . . . . . . .

e. Fonction de Jacobi contenant d'autres constantes que les x⁽⁰⁾_r . . . . . . . . .

5. Champ électromagnétique B_[rs] constant et uniforme . . . . . . . . . . . . . . . . . .

a. Variation de la quadrivitesse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Les équations du mouvement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Les constantes du système . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. L'opérateur d'évolution dans l'espace des phases (matrice symplectique)

e. La fonction de Jacobi S₍₃₎ (x_r , s ; x⁽⁰⁾_r , s₀) . . . . . . . . . . . . . . . . . . . . . .

f. Champ magnétique seul . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6. Potentiel Coulombien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Formules générales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Cas où D < 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Cas où D > 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Cas où D = 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

e. Trajectoires rectilignes (L = 0) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7. L'oscillateur relativiste . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Expression de la vitesse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Loi du mouvement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Module de périodicité de l'action . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8. Particule dans un potentiel W(x_r) qui est un invariant relativiste . . . . . . . . .

a. Premier type d'équation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Deuxième type d'équation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

9. Particule chargée dans une onde électromagnétique plane . . . . . . . . . . . . . .

a. La fonction de Jacobi du type S (x_u , t ; p_u) . . . . . . . . . . . . . . . . . . . . . . .

b. Les équations du mouvement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Calcul du rayonnement de la charge . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Fonction de Jacobi du type S (x_r , s ; p_r , s₀) . . . . . . . . . . . . . . . . . . . . . .

Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

II. Dynamique relativiste quantique des particules de spin zéro
(A. Absence de Champ)

1. L'équation aux dérivées partielles du champ quantique . . . . . . . . . . . . . . . .

a. L'équation de Klein - Gordon . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. L'équation de conservation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Problèmes de conditions initiales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2. Formalisme Lagrangien. Valeurs moyennes et opérateurs . . . . . . . . . . . . . .

a. Expression du Lagrangien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. L'invariance de jauge de première espèce et la charge Q . . . . . . . . . . . .

c. L'invariance pour une translation dans l'espace et le temps :
    Vecteur P_r d'impulsion-énergie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. L'invariance pour une rotation d'espace temps et le tenseur
    antisymétrique J_[rs] du moment cinétique . . . . . . . . . . . . . . . . . . . . . . . . .

e. Définition du produit scalaire et expression générale de la
    valeur moyenne associée à un opérateur O . . . . . . . . . . . . . . . . . . . . . . .

f. Recherche des intégrales premières . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

g. Autres formalismes pour le champ associé à la particule de spin zéro

3. Formalisme Hamiltonien et fonction d'onde à deux composantes complexes

a. Expression de l'opérateur Hamiltonien H . . . . . . . . . . . . . . . . . . . . . . . . .

b. Équation de conservation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. L'opération de conjugaison de charge . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Valeurs moyennes et dérivées par rapport au temps . . . . . . . . . . . . . . . .

e. Transformation des fonctions d'onde F et des opérateurs . . . . . . . . . . . .

f. Diagonalisation de l'Hamiltonien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4. Introduction du temps propre l dans les équations d'ondes . . . . . . . . . . . . .

a. Premier type d'équation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Deuxième type d'équation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5. Les ondes à fréquences positives et négatives et l'espace des
    moments (représentation d'impulsion) . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Système complet des fonctions de base . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Solution générale de l'équation de K.G . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Calcul des valeurs moyennes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Expression des propagateurs à l'aide des fonctions de base . . . . . . . . . .

6. L'équation de K.G. non homogène et les sources de particules . . . . . . . . . .

a. équation de non conservation et le débit des sources . . . . . . . . . . . . . . . .

b. Exemple de sources uniformément distribuées sur le plan z = z₀ . . . . . . .

c. Exemple de sources ponctuelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Les fonctions de Green . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

III. Dynamique relativiste quantique des particules de spin zéro
(B. Présence de Champ)

1. L'équation des ondes et l'équation de conservation . . . . . . . . . . . . . . . . . . .

2. Formalisme Lagrangien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Particule dans un champ donné . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Interaction d'une particule chargée avec le champ électromagnétique . . .

3. Formalisme Hamiltonien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Forme matricielle de l'équation fondamentale . . . . . . . . . . . . . . . . . . . . .

b. Diagonalisation de l'Hamiltonien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. L'équation de conservation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Les valeurs moyennes et leurs équations d'évolution . . . . . . . . . . . . . . . .

4. Introduction du temps propre l . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Premier type d'équation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Deuxième type d'équation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5. L'approximation quasi-classique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Équation de K. G. et fonction de Jacobi S₍₁₎ . . . . . . . . . . . . . . . . . . . . . .

b. Équations des ondes contenant le temps propre
    et fonctions de Jacobi correspondantes . . . . . . . . . . . . . . . . . . . . . . . . . .

6. Potentiels constants, linéaires et quadratiques . . . . . . . . . . . . . . . . . . . . . . .

a. Réflexion sur une barrière de potentiel . . . . . . . . . . . . . . . . . . . . . . . . . .

b. L'oscillateur linéaire relativiste . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Particule dans une induction magnétique uniforme . . . . . . . . . . . . . . . . . .

d. Particule dans un champ électrique uniforme . . . . . . . . . . . . . . . . . . . . . .

e. Détermination du propagateur dans B_(rs) = Cte . . . . . . . . . . . . . . . . . . . .

7. Potentiel Coulombien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Solution approchée par la théorie des perturbations . . . . . . . . . . . . . . . .

b. Solution exacte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Normalisation des fonctions d'onde et valeurs moyennes . . . . . . . . . . . . .

d. Diffusion d'une particule par un potentiel coulombien
    (Approximation de Born) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8. Action d'une onde électromagnétique plane . . . . . . . . . . . . . . . . . . . . . . . . .

Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

IV. Dynamique relativiste classique des particules à spin

1. Champ d'une particule possédant des moments magnétique et électrique . . .

a. Particule au repos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Particule en mouvement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2. Calcul de la force qu'un champ électromagnétique
    exerce sur les dipôles ponctuels . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Particule au repos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Particule en mouvement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3. L'électrodynamique classique non relativiste . . . . . . . . . . . . . . . . . . . . . . . .

a. Formalisme Lagrangien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Formalisme Hamiltonien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Variation du spin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Diffusion d'une onde électromagnétique plane
    par une particule initialement au repos . . . . . . . . . . . . . . . . . . . . . . . . . .

4. Électrodynamique classique relativiste . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Théorie du spin de Thomas (champs constants et homogènes) . . . . . . . . .

b. Théorie du spin dans des champs quelconques . . . . . . . . . . . . . . . . . . . .

c. Particule possédant à la fois un moment magnétique
    et un moment électrique intrinsèques . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Autres théories possibles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

e. Influence du champ propre de la particule . . . . . . . . . . . . . . . . . . . . . . . .

Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

V. Transformation des tenseurs
et des spineurs de l'espace tridimensionnel

1. Transformation des vecteurs (3 composantes) . . . . . . . . . . . . . . . . . . . . . . .

a. La matrice O des transformations orthogonales . . . . . . . . . . . . . . . . . . . .

b. Expression de O sous la forme [] . . . . . . . . . . . . . . . . . . . . . . . . .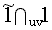

c. Expression de O sous la forme exp (F) . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Vecteurs propres de la matrice (n. S) . . . . . . . . . . . . . . . . . . . . . . . . . . .

e. Les spineurs à 3 composantes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2. Transformation des tenseurs de rang deux (9 composantes) . . . . . . . . . . . . .

a. Expression de la matrice W d'ordre neuf . . . . . . . . . . . . . . . . . . . . . . . . .

b. Réduction de la matrice W . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Représentation spinorielle équivalente . . . . . . . . . . . . . . . . . . . . . . . . . .

3. Transformation des tenseurs de rang n (3ⁿ composantes) . . . . . . . . . . . . . . .

a. Expression de la matrice W d'ordre 3ⁿ . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Réduction de la matrice W . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4. Transformation des spineurs de Pauli (2 composantes) . . . . . . . . . . . . . . . .

a. Définition et propriétés des matrices de Pauli . . . . . . . . . . . . . . . . . . . . .

b. L'équation aux valeurs propres de la matrice (n_us^u) . . . . . . . . . . . . . . . .

5. Transformation des spineurs A (2J + 1) composantes . . . . . . . . . . . . . . . . .

a. Les matrices du spin J . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Équation aux valeurs propres de la matrice (n_uS^u_{(2J + 1)}) . . . . . . . . . . . .

c. Produit de deux représentations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Transformation d'un champ de spineur pour une
    transformation infinitésimale des coordonnées (rotations) . . . . . . . . . . . .

Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

VI. Théorie quantique non relativiste du spin

1. Le spin de l'électron . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Les bases expérimentales de la théorie . . . . . . . . . . . . . . . . . . . . . . . . . .

b. L'équation des ondes de Pauli . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. L'équation de Pauli avec quatre fonctions réelles . . . . . . . . . . . . . . . . . .

d. Électron dans une induction magnétique uniforme et constante . . . . . . . .

e. Électron dans une induction magnétique tournante . . . . . . . . . . . . . . . . . .

f. L'interaction spin-orbite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2. Particule de spin quelconque . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Formalisme Hamiltonien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. L'équation de conservation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Dérivées des grandeurs moyennes ; opérateur vitesse . . . . . . . . . . . . . . .

d. Variation de la vitesse moyenne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

e. Variation du spin moyen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

f. Formalisme Lagrangien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

g. Interaction de la particule avec le champ électromagnétique . . . . . . . . . .

h. Correction relativiste . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

i. Particule au repos dans une induction magnétique uniforme . . . . . . . . . . .

3. Structure fine des niveaux d'énergie des atomes à un électron . . . . . . . . . . .

a. Décomposition des niveaux d'énergie due au spin . . . . . . . . . . . . . . . . . .

b. Autres causes intervenant dans la structure fine . . . . . . . . . . . . . . . . . . . .

c. Les règles de sélection et l'intensité des raies spectrales . . . . . . . . . . . . .

d. Action d'une induction magnétique uniforme B sur la structure fine . . . . .

4. Structure hyperfine des niveaux d'énergie des atomes à un électron . . . . . .

a. Origine du phénomène et perturbation de l'Hamiltonien . . . . . . . . . . . . . .

b. Décomposition des niveaux l = 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. Décomposition des niveaux l ¹ 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Influence d'une induction magnétique B sur la structure hyperfine . . . . . .

5. Effet Stark de la structure fine . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

6. Particules possédant un moment quadrupolaire électrique . . . . . . . . . . . . . .

Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

VII. Notes diverses

1. Quelques identités tensorielles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2. Les valeurs propres et les projecteurs de quelques matrices remarquables

a. Équation aux valeurs propres d'une matrice
    antisymétrique d'ordre quatre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Équation aux valeurs propres d'une matrice du type F_(±) . . . . . . . . . . . .

c. Équation aux valeurs propres de la matrice D . . . . . . . . . . . . . . . . . . . . .

3. Coordonnées dans R₄ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Coordonnées sphériques dans R₄ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Coordonnées hyperboliques dans R₄ . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4. Le propagateur de l'équation de Klein - Gordon (Équation homogène) . . . .

a. Forme intégrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Forme explicite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5. Les fonctions de Green de l'équation de Klein - Gordon . . . . . . . . . . . . . . .

a. Définition et propriétés des fonctions de Green . . . . . . . . . . . . . . . . . . . .

b. La fonction de Green retardée G_R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

c. La fonction de Green avancée G_A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. La fonction de Green causale G_C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

e. La fonction de Green non causale G_N . . . . . . . . . . . . . . . . . . . . . . . . . . .

f. Développement en série de K, K_±, G_R, G_C
   au voisinage du cône de lumière . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

g. Cas où le second membre ne dépend pas du temps . . . . . . . . . . . . . . . . .

6. Le théorème de Noether et les équations de conservation . . . . . . . . . . . . . .

a. Formule générale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

b. Invariance pour une translation infinitésimale dans l'espace et le temps

c. Invariance pour une transformation infinitésimale
    de Lorentz du groupe continu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

d. Invariance pour une transformation de jauge de première espèce . . . . . .

7. Éléments de matrice conduisant aux règles de sélection
    et aux intensités des raies spectrales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

a. Relations de commutation des opérateurs g_u . . . . . . . . . . . . . . . . . . . . . .

b. Condition de non nullité pour les éléments de matrice du vecteur g_u . . . .

c. Action des opérateurs g sur les fonctions d'onde . . . . . . . . . . . . . . . . . . .

d. Action sur les fonctions d'onde d'un opérateur g qui est relié à
    J = J₍₁₎ + J₍₂₎ par les formules (420), (421) et qui commute avec J₍₁₎

1

1

 
3

5

6

6

7

7

7

9

11

12

12

13

14

14

15

16

16

19

23

24

26

28

34

34

36

42

44

44

46

46

47

48

49

49

52

54

54

55

58

60

61

68

68

69

71

72

72

73

 
74

 
75

 
77

79

79

85

85

87

88

89

91

92

95

95

99

 
102

102

103

105

108

111

111

112

115

116

119

122

124

124

125

126

126

127

129

129

131

131

132

134

134

 
144

147

147

150

153

155

157

158

158

160

162

 
163

164

166

170

170

174

 
176

176

186

190

190

193

194

 
196

204

204

214

 
221

228

231

233

238

238

241

243

245

249

250

250

252

257

259

259

259

261

261

263

268

268

271

272

 
273

275

283

283

286

291

293

297

301

303

303

305

306

307

308

309

311

313

313

316

316

320

322

326

334

334

336

339

342

343

349

353

357

359

 
360

370

373

376

376

379

381

381

383

389

389

391

394

396

398

 
398

399

400

400

403

 
404

406

 
406

407

408

411

 
415